Ising Model with Disorder
The main goal during my PhD Thesis was to study the Ising model with long-range power-law correlated site disorder. I will try to explain this model in a few words.
We start with the pure Ising model, i.e., without disorder. Imagine a lattice in two dimensions. On each lattice site you place a spin (arrow) which can have to states, either it points up or down.
The arrows like to point into the same directions as this decreases the total energy of the system. However, due to the thermal fluctuations, they randomly switch their orientation from time to time.If we vary the temperature, we will find two possible states of the system. For low temperatures the fluctuations will become unimportant and (almost) all spins will show into the same direction. For a high temperature, the fluctuation will dominate and the spins will be oriented randomly. The temperature at which the transition from one state to the other happens, is called the critical temperature T_c. The cue now is to study the critical transition from one phase to the other in more detail.
In the case of present disorder, we start to remove some spins on the lattice and by this introduce defects to the lattice.
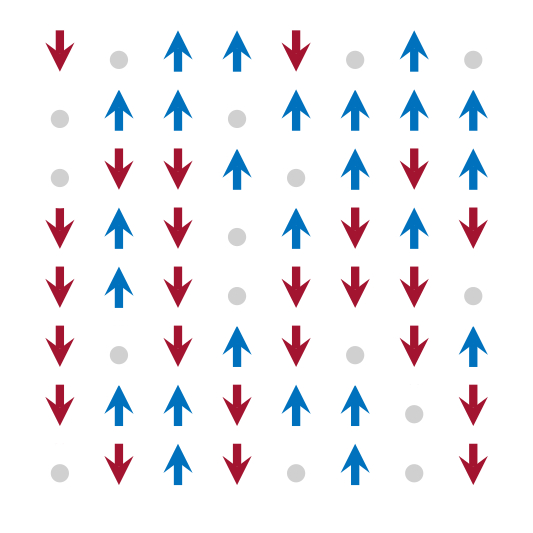
To go one step further, instead of randomly picking the defect sites, we now assume that they are spatially correlated, i.e., they try to form some sort of defect clusters on the lattice.
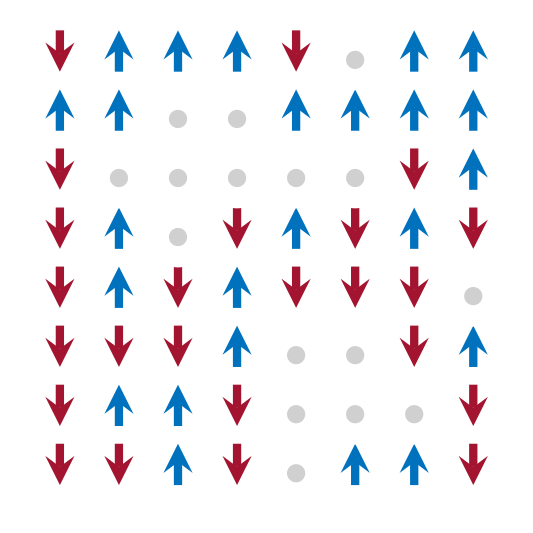
Now, the question arises, how does this disorder affect the critical behavior of the Ising model. This was the question we have studied during my PhD thesis.
Publications
| 2020 | Critical exponent ν of the Ising model in three dimensions with long-range correlated site disorder analyzed with Monte Carlo techniques S. Kazmin and W. Janke In: Phys. Rev. B 102.17 (2020), p. 174206. doi: 10.1103/PhysRevB.102.174206 |
| 2017 | Partially conserved axial vector current and applications R. Horsley, S. Kazmin, Y. Nakamura, H. Perlt, P. Rakow, G. Schierholz, A. Schiller, and J. Zanotti In: Proceedings of 34th annual International Symposium on Lattice Field Theory — PoS (LATTICE2016). 34th annual International Symposium on Lattice Field Theory. University of Southampton, UK: Sissa Medialab, 2017, p. 149. doi: 10.22323/1.256.0149 |